대표적인 복잡도 함수
- Θ(lg n)
- Θ(n) : 1차(linear)
- Θ(n lg n)
- Θ(n 2 ) : 2차(quadratic)
- Θ(n 3 ) : 3차(cubic)
- Θ(2n ) : 지수(exponential)
- Θ(n!)
- Θ(n n)
최고차 항이 최종적으로 전체 영향이 가장 크다.

• Eventually
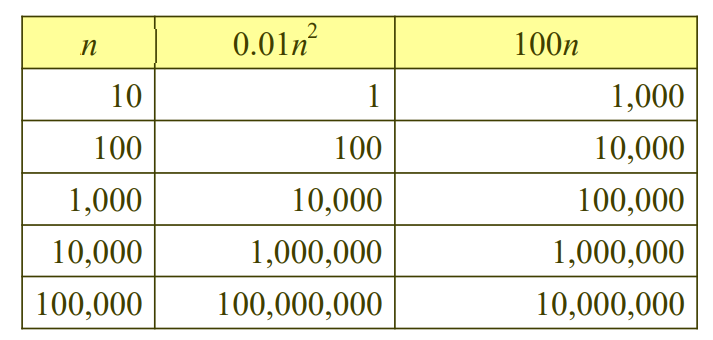
10,000보다 큰 n에 대해서 0.01n^2 > 100n.
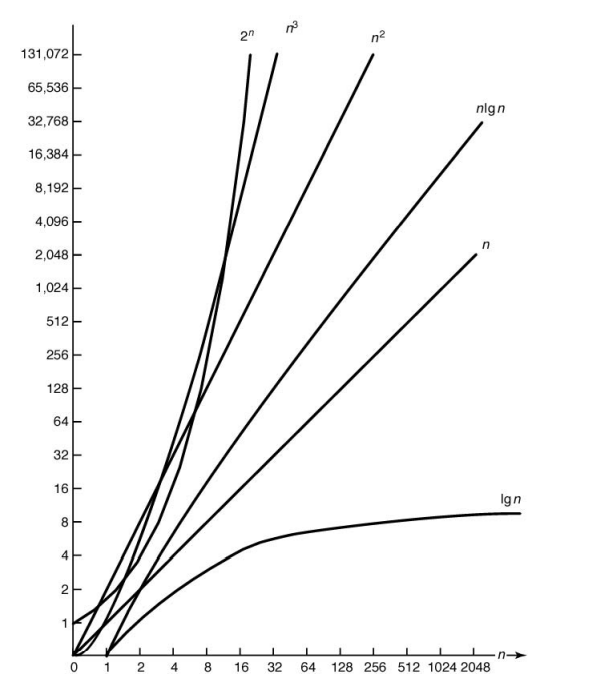
시간복잡도별 실행시간 비교

Asymptotic(점근적) Behavior
- f(n)의 asymptotic behavior는 n이 큰 수가 될 때의 함수 f(n)이 갖는 특성
- (예) f(n) = 1/n

복잡도 함수 표기법
- O( ) - big oh: asymptotic upper bound
- o( ) - small oh: upper bound that is not asymptotically tight
- Ω( ) - omega: asymptotic lower bound
- ω( ) - small omega: lower bound that is not asymptotically tight
- Θ( ) - theta: asymptotic tight bound
큰(big)Ο 표기법
정의 : 점근적 상한(asymptotic upper bound)
- 주어진 복잡도 함수 f(n)에 대해서 g(n)∈Ο(f(n)) 이면 n ≥ N인 모든 정수 n에 대해서 0 ≤ g(n) ≤ c × f(n)이 성립하는 양의 실 수 c와 음이 아닌 정수 N이 존재한다.
- O(f(n)) = {g(n): there exist positive constants c and N such that 0≤ g(n) ≤ c × f(n) for all n ≥ N}
g(n) ∈ Ο(f(n)) 읽는 방법:
- g(n)은 f(n)의 큰 오(big Ο)
큰 Ο 표기법

큰 Ο 표기법
어떤 함수 g(n)이Ο(n 2 )에 속한다는 말은
- 그 함수는 n이 커짐에 따라 (즉, 어떤 임의의 N값보다 큰 값에 대해서는) 어떤 2차 함수 cn 2 보다는 작은 값을 가지게 된다는 것을 뜻한다. (그래프 상에서는 아래에 위치)
- 그 함수 g(n)은 어떤 2차 함수 cn 2 보다는 궁극적으로 좋다고 (빠르다) 말할 수 있다.
어떤 알고리즘의 시간복잡도가 Ο(f(n))이라면
- 입력의 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 늦 어도 cf(n)은 된다. (cf(n)이 점근적상한이다.)
- 이 알고리즘의 수행시간은 cf(n)보다 절대로 더 느릴 수는 없다.
큰 Ο 표기법 : 예
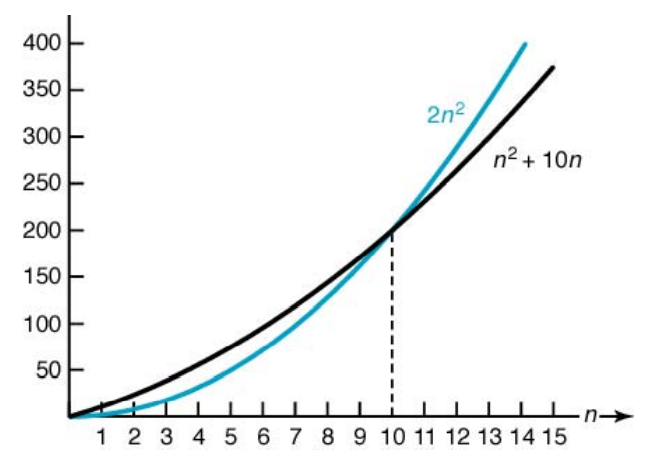
n^2 +10n ∈ Ο(n^2 ) ?
(1) n ≥ 10인 모든 정수 n에 대해서 n^2 +10n ≤ 2n^2 이 성립. 그러므로, c = 2 와 N = 10을 선택하면, “큰 Ο ”의 정의에 의해서 n^2 +10n ∈ Ο(n^2).
(2) n ≥ 1인 모든 정수 n에 대해서 n^2 +10n ≤ n^2 +10n^2 = 11n^2 이 성립. 그러 므로, c = 11와 N = 1을 선택하면, “큰 Ο ”의 정의에 의해서 n^2 +10n ∈ Ο(n^2).
2n^2 과 n^2 + 10n의 비교
5n^2 ∈ Ο(n^2 ) ? c=5와 N=0을 선택하면, n ≥ 0인 모든 정수 n에 대해서 5n 2 ≤ 5n 2 성립.

n ≥ 0인 모든 정수 n에 대해서

이 성립. 그러므로, c = 1/2 와 N=0을 선택하면, T(n) ∈Ο(n 2 ).
n^2 ∈ Ο(n^2 +10n) ? n ≥ 0인 모든 정수 n에 대해서, n^2 ≤ 1× (n^2 +10n)이 성립. 그러므로, c=1와 N=0을 선택하면, n^2 ∈ Ο(n^2 +10n).
n ∈ Ο(n^2) ? n ≥ 1인 모든 정수 n에 대해서, n ≤ 1×n 2 이 성립. 그러므로, c=1와 N=1을 선택하면, n ∈Ο(n^2 ).
n^3 ∈ Ο(n^2) ?
n ≥ N인 모든 n에 대해서 n^3 ≤ c×n^2 이 성립하는 c와 N 값은 존재하지 않 는다. 즉, 양변을 n^2 으로 나누면, n ≤ c 가 되는데 c를 아무리 크게 잡더라 도 그 보다 더 큰 n이 존재한다. 그러므로

Ο (n^2)

Ω 표기법
정의 : 점근적 하한(asymptotic lower bound)
- 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ Ω(f(n))이면 n ≥ N인 모든 정수 n에 대해서 g(n) ≥ c × f(n) ≥ 0이 성립하는 양의 실수 c 와 음이 아닌 정수 N이 존재한다.(Big O와 반대)
- Ω(f(n)) ={g(n): there exist positive constants c and N such that g(n) ≥ c × f(n) ≥ 0 for all n ≥ N}
g(n) ∈ Ω(f(n)) 읽는 방법: − g(n)은 f(n)의 오메가(omega)

어떤 함수 g(n)이 Ω(n^2 )에 속한다는 말은
- 그 함수는 n이 커짐에 따라 (즉, 어떤 임의의 N 값보다 큰 값에 대해서 는) 어떤 2차 함수c^2 의 값보다는 큰 값을 가지게 된다는 것을 뜻한다. (그래프 상에서는 위에 위치)
- 그 함수 g(n)은 어떤 2차 함수 cn^2 보다는 궁극적으로 나쁘다고 (느리 다)말할 수 있다.
어떤 알고리즘의 시간복잡도가 Ω(f(n))이라면,
- 입력의 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 빨라도 cf(n)밖에 되지 않는다. (cf(n)이 점근적하한이다.)
- 이 알고리즘의 수행시간은 cf(n)보다 절대로 더 빠를 수는 없다.
n^2 +10n ∈ Ω(n^2 ) ?
- n ≥ 0인 모든 정수 n에 대해서 n^2 +10n ≥ n^2 이 성립한다. 그러므로, c = 1 와 N = 0을 선택하면, n^2 +10n ∈ Ω(n^2 ).
5n^2 ∈ Ω(n^2 ) ?
- n ≥ 0인 모든 정수 n에 대해서, 5n^2 ≥ 1×n^2 이 성립한다. 그러므로, c = 1와 N = 0을 선택하면, 5n^2∈Ω(n^2).



Θ 표기법
정의 : (asymptotic tight bound)
- 복잡도 함수 f(n) 에 대해서 Θ(f(n))= O(f(n))∩ Ω(f(n))
- n ≥ N 인 모든 정수 n 에 대해서 c × f(n) ≤ g(n) ≤ d × f(n)이 성립하는 양의 실수 c와 d, 음이 아닌 정수 N이 존재한다.
- Θ(f(n))={g(n): there exist positive constants c, d, and N such that c × f(n) ≤ g(n) ≤ d × f(n) for all n ≥ N}
참고: g(n) ∈ Θ(f(n))은 “g(n)은 f(n)의 차수(order)”라고 한다.
예 : T(n) = O(n(n-1)/2)은 O(n^2)이면서 Ω(n^2 )이다. 따라서



작은(small) Ο 표기법
작은 o는 복잡도 함수끼리의 관계를 나타내기 위한 표기법이다.
정의 : 작은 o
주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ o(f(n))이면 모든 양의 실수 c에 대해, n ≥ N인 모든 n 에 대해서 0 ≤ g(n) ≤ c × f(n) 이 성 립하는 음이 아닌 정수 N 이 존재한다.
- o(f(n))={g(n): for any positive constants c>0, there exists a constant N>0 such that 0 ≤ g(n) ≤ c × f(n) for all n ≥ N}
참고: g(n) ∈o(f(n)) 은 “g(n)은 f(n)의 작은 오(o)”라고 한다.

큰 Ο vs.작은 o
큰 Ο와의 차이점
- 큰 Ο - 실수 c > 0 중에서 하나만 성립하여도 됨
- 작은 o - 모든 실수 c > 0에 대해서 성립하여야 함
g(n) ∈o(f(n))은 g(n) 이 궁극적으로 cf(n)보다 훨씬 낫다(좋다, 작은 값)는 의미이다.
작은 o 표기법 : 예
n ∈ o(n^2 ) ?
증명:
- c > 0이라고 하자. n ≥ N인 모든 n에 대해서 n ≤ cn2 이 성립하는 N 을 찾아야 한다.
- 이 부등식의 양변을 cn으로 나누면 1/c ≤ n 을 얻는다.
- 따라서 N ≥ 1/c가 되는 어떤 N 을 찾으면 된다.
- 여기서 N 의 값은 c에 의해 좌우된다.
- 예를 들어 만약 c=0.0001 이라고 하면, N 의 값은 최소 10,000이 되어 야 한다.
- 즉, n >10,000인 모든 n에 대해서 n ≤ 0.0001n2 이 성립한다.
n ∈ o(5n) ?
모순 유도에 의한 증명:
- c=1/6 이라고 하자.
- n ∈ o(5n)이라고 가정하면, n ≥ N인 모든 정수 n에 대해서, n ≤ 1/6 ×5n = 5/6n이 성립하는 음이 아닌 정수 N이 존재해야 한다.
- 그러나 그런 N은 절대로 있을 수 없다.
- 따라서 위의 가정은 모순이다.

차수의 주요 성질
1. g(n) ∈O(f(n)) if and only if f(n) ∈Ω(g(n))
2. g(n) ∈Θ(f(n)) if and only if f(n) ∈Θ(g(n))
3. b > 1이고 a > 1이면, loga n ∈ Θ(logb n)은 항상 성립. 즉, 로그(logarithm) 복 잡도 함수는 모두 같은 카테고리에 속한다. 따라서 통상 Θ(lg n)으로 표시 한다.
4. b > a > 0이면, a^n ∈ o(b^n ). 즉, 지수(exponential) 복잡도 함수가 모두 같은 카테고리 안에 있는 것은 아니다.
5. a > 0인 모든 a에 대해서, a^n ∈ o(n!). 다시 말하면, n!은 어떤 지수 복잡도 함수보다도 나쁘다.
6. 복잡도 함수를 다음 순으로 나열해 보자.

여기서 k>j>2이고 b>a>1이다. 복잡도함수 g(n)이 f(n)을 포함한 카테고리의 왼 쪽에 위치한다고 하면, g(n)∈ o(f(n))
7. c ≥ 0, d ≥ 0, g(n)∈Ο( f (n)), 그리고 이면, c× g(n)+ d × h(n)∈Θ( f (n))
극한(limit)를 이용하여 차수를 구하는 방법




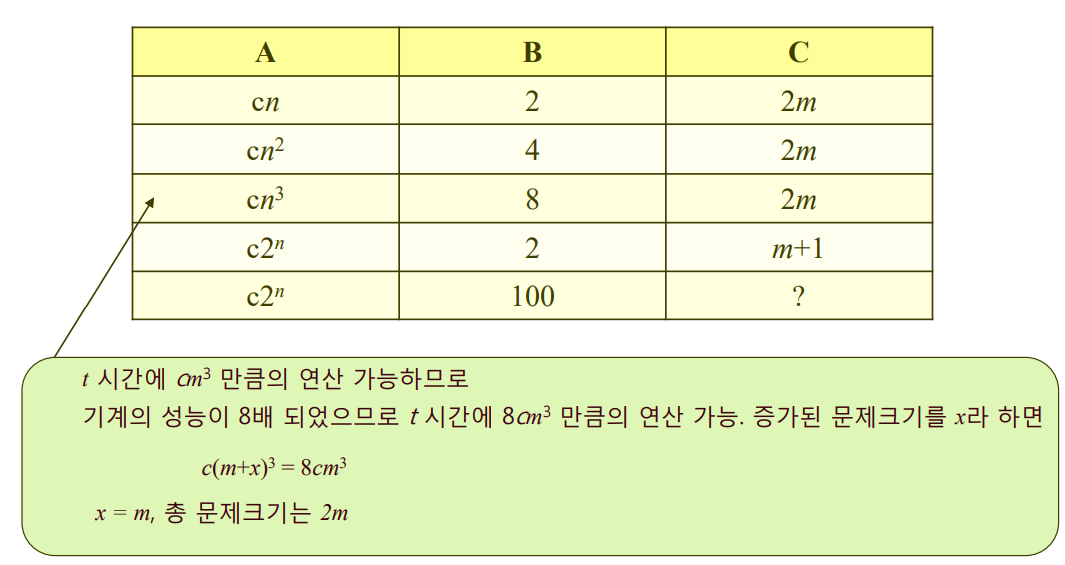
알고리즘 복잡도와 컴퓨터 능력
1.알고리즘의 복잡도가 cn일 때 t시간 동안
- 현재의 기계가 문제크기 m개의 문제 해결
- 기계의 처리 속도가 2배 된다면 문제크기 2m개의 문제를 t시간에 해결할 수 있다.
2. 알고리즘의 복잡도가 cn2일 때 t시간 동안
- 현재의 기계가 문제크기 m개의 문제 해결
- 기계의 처리 속도가 4배 된다면 문제크기 2m개의 문제를 t시간에 해결할 수 있다.
3. 알고리즘의 복잡도가 c2n일 때 t시간 동안
- 현재의 기계가 문제크기 m개의 문제 해결
- 기계의 처리 속도가 2배 된다면 문제크기 m+1개의 문제를 t시간에 해결할 수 있다.
- 기계의 처리 속도가 100배 된다면 문제크기 ??개의 문제를 t시간에 해결할 수 있다.
알고리즘 복잡도와 컴퓨터 능력
- 알고리즘의 복잡도가 (A)일 때 t시간 동안
- 현재의 기계가 문제크기 m개의 문제 해결
- 기계의 처리 속도가 (B)배 된다면 문제크기 (C)개의 문제를 t시간에 해결할 수 있다.

'👨💻Computer Science > 알고리즘 분석' 카테고리의 다른 글
| [알고리즘 분석] 02 - 3 빠른정렬(Quicksort) (0) | 2021.09.23 |
|---|---|
| [알고리즘 분석] 02 - 2 합병정렬(mergesort) (0) | 2021.09.16 |
| [알고리즘 분석] 02 - 1 분할정복법(divide-and-conquer) (0) | 2021.09.16 |
| [알고리즘 분석] 01 - 2 알고리즘의 분석(analysis) (0) | 2021.09.14 |
| [알고리즘 분석] 01 - 1 알고리즘: 효율, 분석 그리고 차수 (0) | 2021.09.02 |




댓글